Question

How do you calculate the wavelength of the light emitted by a hydrogen atom during a transition of its electron from the n = 4 to the n = 1 principal energy level? Recall that for hydrogen En=−2.18×10^−18J(1/n^2)

Answer 1

Wavelength,
`\lambda=9.75* 10^(-8)\ m`

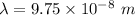
Step-by-step explanation:

We need to find the the wavelength of the light emitted by a hydrogen atom during a transition of its electron from the n = 4 to the n = 1 principal energy level. The energy is given by :

`\Delta E=E_1-E_4`

`\Delta E=-2.18* 10^(-18)((1)/(n_f^2)-(1)/(n_i^2))`

`\Delta E=-2.04* 10^(-18)\ J`

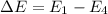
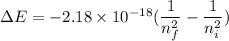
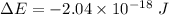
The energy of a photon is given by :

`E=(hc)/(\lambda)`

`\lambda=(hc)/(E)`

`\lambda=(6.63* 10^(-34)* 3* 10^8)/(2.04* 10^(-18))`

`\lambda=9.75* 10^(-8)\ m`

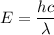
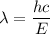
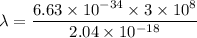
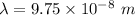
So, the wavelength of the light emitted by a hydrogen atom during a transition of its electron from the n = 4 to the n = 1 principal energy level is
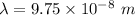`\lambda=9.75* 10^(-8)\ m`. Hence, this is the required solution.