Answer:
Power generated will be equal to 1054.046 watt
Step-by-step explanation:
We have given mass m = 0.129 kg
Length of the rope = 3.70 m
So mass density
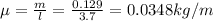
Amplitude A = 0.200 m
Wavelength = 0.600 m
Velocity of the wave v = 24 m/sec
So frequency
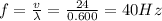
Now angular frequency will be equal to
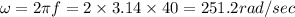
We have to fond the generated power
Power will be equal to
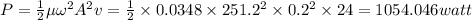
So power generated will be equal to 1054.046 watt