Question

A 5 kg fish swimming at 1 m/s swallows an absentminded 500 g fish swimming toward it at a velocity that brings both fish to a halt immediately after lunch. What is the velocity of the approaching smaller fish before lunch?

Answer 1

To solve this problem we will apply the concepts related to the conservation of momentum. Momentum is defined as the product between mass and velocity of each body. And its conservation as the equality between the initial and final momentum. Mathematically described as

`m_1u_1+m_2u_2 = (m_1+m_2)v_f`

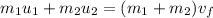
Here

`m_1` = Mass of big fish

`m_2` = Mass of small fish

`v_1` = Velocity of big fish

`v_2` = Velocity of small fish

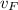`v_F` = Final Velocity

The big fish eats small fish and the final velocity is zero. Rearrange the equation for the initial velocity of small fish we have

`m_1u_1=-m_2u_2`

`u_2 = -(m_1u_1)/(m_2)`

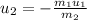
Replacing we have,

`u_2 = -((5kg)(1m/s))/(0.5kg)`

`u_2 = -10m/s`

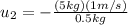
The negative sign indicates that the small fish is swimming in the direction opposite to that of the big fish.

Therefore the speed of the small fish is 10m/s