Question

For this problem, prove/derive the formula that allows one to find an expected value for X by conditioning on Y :

Answer 1

`E[X |Y=y] = \int_(-\infty)^(\infty) x f_(X,Y) (x|y) dx`

`E[X|Y=y] =\sum_(x) x f_(X,Y) (x|y)`

Explanation:

For this case we assume that we have two random variable X and Y continuous, and we define the conditional density of X given Y like this:

`f_(X|Y) (x|y) = (f_(X,Y) (x,y))/(f_Y (y))`

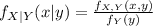
Where
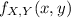`f_(X,Y) (x,y)` is the joint density function. And we can define the conditional probability like this:

`P(a\leq X \leq b | Y = y) = \int_(a)^b f_(X,Y) (x|y) dx`

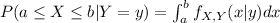
In order to find the expected value of X given Y=y we just need to find this:

`E[X | Y=y] = \int_(-\infty)^(\infty) x f_(X,Y) (x|y) dx`

And if we assume that the random variable is discrete then the conditional expectation would be given by:

`E[X|Y=y] =\sum_(x) x f_(X,Y) (x|y)`

And as we can se just change the integral by a sum over the values defined for X, and with this we have the general formulas in order to find the conditional expectation of X given Y=y for the possible cases for a random variable.