Answer:
see explanation
Explanation:
The sum of the 3 angles in a triangle = 180°
Subtract the sum of the given angles from 180 for A
A = 180° - (90 + 46)° = 180° - 136° = 44°
----------------------------------------------------------------
tan46° =
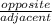 =
=

Multiply both sides by 23
23 × tan46° = b, thus
b ≈ 23.8 ( to the nearest tenth )
-----------------------------------------------------------------
cos46° =
 =
=
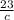
Multiply both sides by c
c × cos46° = 23 ( divide both sides by cos46° )
c =
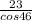 ≈ 33.1 ( to the nearest tenth )
≈ 33.1 ( to the nearest tenth )