A. True. The range of f(x) is
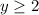 meaning that y cannot be smaller than 2.
meaning that y cannot be smaller than 2.
-------
B. True. Normally
 is not restricted in the domain as any real number will work for x, but we apply a restriction on f(x) so the inverse
is not restricted in the domain as any real number will work for x, but we apply a restriction on f(x) so the inverse
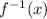 is possible. This is so the graph of f(x) is one-to-one; otherwise, the graph of f(x) fails the horizontal line test.
is possible. This is so the graph of f(x) is one-to-one; otherwise, the graph of f(x) fails the horizontal line test.
-------
C. False. The graph of f(x) is entirely above the x axis, so there are no x intercepts. Alternatively, plug x = 2 into f(x) and you'll find that f(2) does not equal 0.
-------
D. False. The leading coefficient is positive, so the parabola opens upward. Consequently, this means that there is a lowest point (aka minimum) but there is no maximum point as the graph of f(x) goes upward forever.
-------
E. True. Plug in x = 0 and you'll get f(0) = 2. This is where the curve crosses the y axis.
==================================
To summarize, the three answers are: A, B, and E