Answer:
- Constant.
- Linear
Explanation:
Te Rate of change of a line is also known as "Slope" and it is constant.
It is important to remember that, by definition, this is given by:
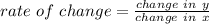
It can be also written as:

Let's substitute into
 the following points:
the following points:
1) Points (1,11) and (2,22)
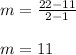
2) Points (2,22) and (3,33):
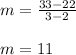
3) Points (3,33) and (4,44):
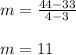
As you can notice, the rate of change (or the slope) of the function given in the table, is always constant.
Therefore you can conclude that it is a Linear Function.