Answer:
(A)
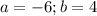
(B)
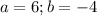
Explanation:
The equation of the line in Slope-Intercept form is:
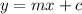
Where "m" is the slope and "c" is the y-intercept.
By definition:
1. If the lines of the System of equations are parallel (which means that they have the same slope), the system has No solutions.
2. If the they are the same exact line, the System of equations has Infinite solutions.
Given the following System of Linear equations:
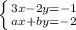
(A) Let's solve for "y" from the first equation:
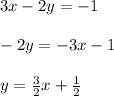
You can notice that:
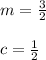
Then, in order make that the System has No solutions, the slopes must be the same, but the y-intercept must not.
Then, the values of "a" and "b" can be:
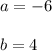
Substituting those values into the second equation and solving for "y", you get:
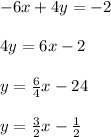
You can idenfity that:
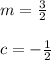
Therefore, they are parallel.
(B) In order make that the System has Infinitely many solutions, the slopes and the y-intercepts must be the same.
Then, the values of "a" and "b" can be:
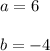
If you substitute those values into the second equation and then you solve for "y", you get:
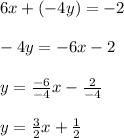
You can identify that:
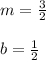
Therefore, they are the same line.