Question

A pipe can fill a pool in 12 hours. Another pipe can fill the pool in 18 hours. How long will it take for the two pipes to fill the pool if they operate simultaneously?

Answer 1

It takes 7.2 hours for the two pipes to fill the pool if they operate simultaneously

Solution:

Given that,

A pipe can fill a pool in 12 hours

Thus, in one hour first pipe does
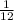`(1)/(12)` of the job

Another pipe can fill the pool in 18 hours

Thus, in one hour second pipe does
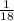`(1)/(18)` of the job

Therefore, we can say,

In "x" hours, first pipe does
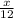`(x)/(12)` of the job

In "x" hours, second pipe does
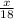`(x)/(18)` of the job

Working together they do the one job.

Thus, we get,

`(x)/(12) + (x)/(18) = 1\\\\x((1)/(12) + (1)/(18)) = 1\\\\x((12+18)/(12 * 18)) = 1\\\\x((30)/(216)) = 1\\\\x = (216)/(30)\\\\x = 7.2`

Thus, it takes 7.2 hours for the two pipes to fill the pool if they operate simultaneously