Question

How do I solve this question?

Answer 1

m=2 and n=3

Explanation:

Step :-

Given
`[ 2 x^(n)y^(2) ]^m = 4 x^6 y^4`

using algebraic formula
`(a^m)^n= a^(mn)`

now

`2^(m) x^(mn) y^(2m) = 4x^(6) y^(4)`

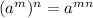
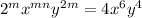
now equating 'x' powers, we get

`x^(mn) = x^(6)`

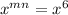
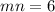`mn=6` ....(1)

now

`y^(2m) = y^(4)`

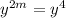
Equating 'y' powers ,we get

2 m=4

m=2

substitute m= 2 in equation (1)

we get

2 n=6

n=3

verification:-

substitute m=2 and n=3 , we get

`[ 2 x^(n)y^(2) ]^m = 4 x^6 y^4`

`(2 x^(3) y^2)^2 = 4 x^6 y ^4\\`

`4 x^6 y^4 = 4 x^6 y^4`

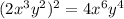
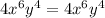
both are equating so m= 2 and n=3