Question

Point X is at 2/3 on a number line.On the same number line,point Y is the same distance from 0 as point X ,but has a numerator of 8. What is the denominator of the fraction at point Y? Draw a number line to model the problem

Answer 1

The denominator of the fraction y = 12.

Explanation:

Given that Point X is at
`$ (2)/(3) $` of a number line. And that the distance between point X and 0 is the same as Y and 0.

Also, it is known that the numerator of Y = 8.

Let us assume
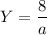`$ Y = (8)/(a) $`, where 'a' is the denominator of the fraction Y.

Since, they are equidistant from 0, we can write:

`$ d(0, X) = d(Y, 0) $`

`$ \implies |X - 0| = |Y - 0| $`

`$ \implies |X| = |Y|$`

`$ \implies (2)/(3) = (8)/(a) $`

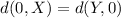
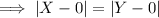
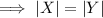
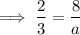
Solving for 'a',

`$ a = (8. 3)/(2) = (24)/(2) = \textbf{12} $`

Therefore, the denominator of the fraction is 12.

NOTE: The fraction
`$ (2)/(3) $` =
`$ (8)/(12) $`

`$ (2. 4)/(3. 4) = (8)/(12) = (2)/(3) $`

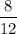
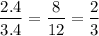
So, 2/3 was multiplied by a factor of 4. We could have arrived at 12, in this way as well,