Answer: 1800
Explanation:
Given : A certain system has two components.
Number of different models of the first component = 6
Number of different models of the second component = 10
A salesman must select 2 of the first component and 3 of the second to take on a sales call , so we use combinations ( ∵ order of selection not matters)
The number of different sets of components can the salesman take =
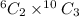
![(6!)/(2!(6-2)!)*(10!)/(3!(10-3)!)\ \ [\because\ ^nC_r=(n!)/(r!(n-r)!)]](https://img.qammunity.org/2021/formulas/mathematics/college/4ojh17ylsmmx99nhr48c4ysd4uctz4hh1u.png)
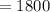
Hence, the number of different sets of components can the salesman take = 1800