Question

One golfer's scores for the season are 88, 90, 86, 89, 96, and 85. Another

golfer's scores are 91, 86, 88, 84, 90, and 83. What are the range and mean of
each golfer's scores? Use your results to compare the golfers' skills.

Answer 1

Mean of the first golfer = 89

Mean of the second golfer = 87

Range of the first golfer = 11

Range of the second golfer = 8

Step-by-step explanation:

First golfer scores 88, 90, 86, 89, 96 and 85.

Sum of the scores of first golfer = 88 + 90 + 86 + 89 + 96 + 85 = 534

Number of observation of first golfer = 6

`\text {Mean} = \frac{\text {Sum of the observation}}{\text {Number of observation}}`

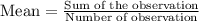
Mean of the first golfer =
`(534)/(6)=89`

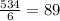
Mean of the first golfer = 89

Range of the first golfer = Highest score – Lowest score

= 96 – 85

Range of the first golfer = 11

Second golfer scores 91, 86, 88, 84, 90 and 83.

Sum of the scores of second golfer = 91 + 86 + 88 + 84 + 90 + 83 = 522

Number of observation of second golfer = 6

`\text {Mean} = \frac{\text {Sum of the observation}}{\text {Number of observation}}`

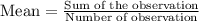
Mean of the second golfer =
`(522)/(6)=87`

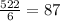
Mean of the second golfer = 87

Range of the second golfer = Highest score – Lowest score

= 91 – 83

Range of the second golfer = 8

Comparing the golfer's skills:

Mean of first golfer is greater than Mean of second golfer. (i.e. 89 > 87)

Range of first golfer is greater than Range of second golfer. (i.e. 11 > 8)

Thus, first golfer have more skills than second golfer.