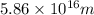The question is incomplete, here is the complete question:
How do you calculate the wavelength of the light emitted from a mole of photons as they transition from the n = 4 to the n = 1 principal energy level in the hydrogen atom. Recall that for hydrogen
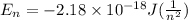
Answer: The wavelength of 1 mole of photons for the given transition is
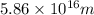
Step-by-step explanation:
To calculate the change in energy, we use the equation:
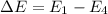
Or,

where,
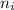 = initial energy level = 4
= initial energy level = 4
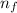 = final energy level = 1
= final energy level = 1
Putting values in above equation, we get:
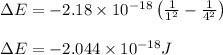
To calculate the wavelength of light for 1 mole of photons, we use the equation:
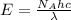
where,
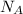 = Avogadro's number =
= Avogadro's number =

h = Planck's constant =
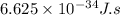
c = speed of light =
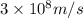
 = wavelength of light = ?
= wavelength of light = ?
E = energy emitted =
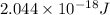
Putting values in above equation, we get:
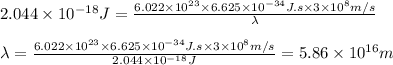
Hence, the wavelength of 1 mole of photons for the given transition is