Question

(a) Determine the required delta-v, Ave, to the nearest m/s, to reach a circular 500 km altitude equatorial prograde (eastward) orbit from a launch site on the Equator of the Earth. Assume the required velocity change is applied instantaneously at launch and neglect the effects of drag and any perturbation forces other than central gravity (b) If one instead wants to launch from the same Equatorial site into a circular 500 km altitude polar orbit, determine the required delta-v, Avp, to the nearest m/s.

Answer 1

a) v₁ = 8.20 10³ m / s , b) v₁’= 8.4 10³ m / s

Step-by-step explanation:

a) For this exercise we can use energy conservation, in two points

Initial. On the earth's surface

Em₀ = K + U = ½ m v₁² - G m Me / Re²

Final. In the orbit at a height of h = 500 10³m

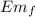`Em_(f)` = K + U = ½ m v₂² - G m Me / (Re+h)²

Em₀ =
`Em_(f)`

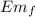
½ m v₁² - G m Me / Re² = ½ m v₂² - G m Me / (Re+h)²

½ v₁² - ½ v₂² = G Me (1 / Re² - 1 / (Re + h)²)

To find the speed of the rocket in orbit we use Newton's sunga law, where force is the force of gravitation

F = m a

The acceleration is centripetal

a = v² / r

G m Me / (Re+h) 2 = m v2 / (Re+h)

v₂² = G Me / (Re + h)

Let's calculate

v² = √ (6.67 10⁻¹¹ 5.98 10²⁴ / (6.37 10⁶ +0.5 10⁶)

v² = √ 58.05909 10⁶

v₂ = 7.62 10³ m / s

Now we can find the clearance speed (v1)

v₁² = 2 G Me (1 / Re2 - 1 / (Re + h) 2) + v₂²

Let's calculate

v₁² = 2 6.67 10⁻¹¹ 5.98 10²⁴ (1 / 6.37 10⁶ - 1 / 6.87 10⁶) + 58.059 10⁶

v₁² = 0.91145 10⁷ + 5.8059 10⁷

v₁ = √ 67.172 10⁶

v₁ = 8.20 10³ m / s

b) If the same place is launched into a polar orbit, the fundamental change is the distance that we can enter using the Pythagorean theorem.

h’= √ 500 + 5002 = 500 √2

h’= √ 2 0.5 10⁶ m

Re + h’= 6.37 10⁶ + √2 0.5 10⁶

Re + h’= 7.077 10⁶ m

Calculate

v₁²’= 2 6.67 10⁻¹¹ 5.98 10²⁴ (1 / 6.37 10⁶ - 1 / 7.077 10⁶) + 58.059 10⁶

v₁²’= 1,251 10⁷ + 5,8059 10⁷

v₁’= 8.4 10³ m / s