Question

Find the equation of a straight line that is perpendicular to 5x–y=1 and is such that the area of the triangle formed by the x- and y-axes is equal to 5.

Answer 1

Answer:
`y = -(1)/(5)x+√(2)`

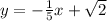
This is approximately the same as
`y = -(1)/(5)x+1.41`

===============================================

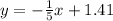
Step-by-step explanation:

Solve the given equation for y

5x-y = 1

-y = -5x+1

y = 5x-1

slope of this line is m = 5 since it is in the form y = mx+b

Write m = 5 as m = 5/1

Flip the fraction: 5/1 ----> 1/5

Flip the sign: 1/5 ----> -1/5

The perpendicular slope is -1/5

---------------------------

Let p and q be the x and y intercepts

So the equation we're after goes through the points (p,0) and (0,q)

The slope of the line through these points is

m = (y2-y1)/(x2-x1)

m = (q-0)/(0-p)

m = q/(-p)

m = -q/p

We want this slope to be -1/5 as this is the perpendicular slope we found earlier

-q/p = -1/5

q/p = 1/5

5q = 1p

p = 5q ... we will use this later

---------------------------

The base of the triangle is p while the height is q

We want the area of the triangle to be 5 square units

area = 0.5*base*height

5 = 0.5*p*q

5 = 0.5*(5q)*q ... plug in p = 5q

5 = 2.5q^2

2.5q^2 = 5

q^2 = 5/2.5

q^2 = 2

q = sqrt(2)

p = 5*q

p = 5*sqrt(2)

The y intercept is b = q = sqrt(2), so

y = mx+b

`y = -(1)/(5)x+√(2)`

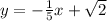
See the diagram below.