Question

Water enters the turbine of an ideal Rankine cycle as a superheated vapor at 18 MPa and 550°C. If the condenser pressure is 9 kPa, find: (a) the rate of heat addition into the cycle, in kJ/kg of water flowing, (b) the thermal efficiency of the system, (c) the rate of heat rejection from the cycle, in kJ/kg of water flowing, (d) the back work ratio.

Answer 1

For this ideal Rankine cycle:

A) The rate of heat addition into the cycle Qh is 3214.59KJ/Kg.

B) The thermal efficiency of the system εt=0.4354.

C) The rate of heat rejection from the cycle Qc is 1833.32KJ/Kg.

D) The back work ratio is 0.013

Step-by-step explanation:

To solve the ideal Rankine cycle we have to determinate the thermodynamic information of each point of the cycle. We will use a water thermodynamic properties table. In an ideal Rankine cycle, the process in the turbine and the pump must be isentropic. Therefore S₃=S₄ and S₁=S₂.

We will start with the point 3:

P₃=18000KPa T₃=550ºc ⇒ h₃=3416.12 KJ/Kg S₃=6.40690 KJ/Kg

Point 4:

P₄=9KPa S₄=S₃ ⇒ h₄=2016.60 (x₄=0.7645 is wet steam)

Point 1:

P₁=P₄ in the endpoint of the steam curve. ⇒ h₁= 193.28KJ/Kg S₁=0.62235KJ/Kg x₁=0

Point 2:

P₂=P₃ and S₂=S₁ ⇒ h₂=201.53KJ/Kg

With this information we can obtain the heat rates, the turbine, and the pump work:

`Q_h=Q_(2-3)=h_3-h_2=3214.59KJ/Kg`

`Q_c=Q_(4-1)=h_4-h_1=1833.32KJ/Kg`

`W_(turb)=W_(3-4)=h_3-h_4=1399.52KJ/Kg`

`W_(pump)=W_(1-2)=h_2-h_1=18.25KJ/Kg`

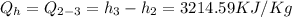
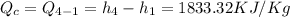
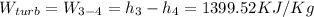
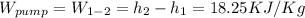
We can answer the questions with this data:

A)
`Q_h=Q_(2-3)=h_3-h_2=3214.59KJ/Kg`

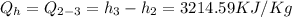
B)
`\epsilon_(ther)=\displaystyle(W_(turb))/(Q_h)=0.4354`

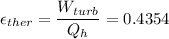
C)
`Q_c=Q_(4-1)=h_4-h_1=1833.32KJ/Kg`

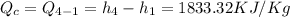
D)
`r_(bW)=\displaystyle(W_(pump))/(W_(turb))=0.013`