What is the fully simplified answer to sqrt(7/18) + sqrt(5/8) - sqrt(7/2)

Question

asked Aug 3, 2021 99.6k views

1 Answer

Moein Hosseini · Answer 1 · 2021-08-10T09:00:25+0000

Answer:

=(-4√(7)+3√(5))/(6√(2))

Explanation:

Given expression as:

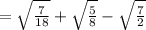
$=\sqrt{(7)/(18)}+\sqrt{(5)/(8)}-\sqrt{(7)/(2) }$

We need to simplify the given expression.

Solution:

We have:

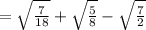
$=\sqrt{(7)/(18)}+\sqrt{(5)/(8)}-\sqrt{(7)/(2) }$

Rewrite the expression as:

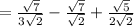
=(√(7))/(3√(2)) - (√(7))/(√(2)) +(√(5))/(2√(2))

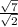(√(7))/(√(2) ) is a common factor to the first two terms.

Using distributive property we can factor out
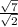(√(7))/(√(2) ) from the first two terms.

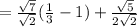
=(√(7))/(√(2))((1)/(3) -1) +(√(5))/(2√(2))

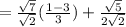
=(√(7))/(√(2))((1-3)/(3)) +(√(5))/(2√(2))

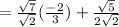
=(√(7))/(√(2))((-2)/(3)) +(√(5))/(2√(2))

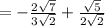
=-(2√(7))/(3√(2)) +(√(5))/(2√(2))

√(2) is common factor, so we can factor
√(2) from the above expression.

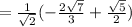
=(1)/(√(2) )( -(2√(7))/(3) +(√(5))/(2))

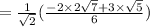
=(1)/(√(2) )( (-2* 2√(7)+3* √(5))/(6))

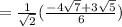
=(1)/(√(2) )( (-4√(7)+3√(5))/(6))

=(-4√(7)+3√(5))/(6√(2))

Therefore, we get simplified answer as.

=(-4√(7)+3√(5))/(6√(2))