Answer:

Explanation:
We are given the following in the question:
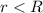
where r and r are the radius of the circle.
General equation of circle:
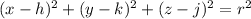
where(h,k,j) is the center of the circle and r is the radius of circle.
If the circle is centered at origin, then,

Equation of circle with radius R centered on origin
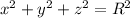
Inequality to describe the region that consist of all points lying between the sphere of radius r and R but not on the sphere is given by:
