Question

A computer company claims that the batteries in its laptops last 4 hours on average. A consumer report firm gathered a sample of 16 batteries and conducted tests on this claim. The sample mean was 3 hours 50 minutes, and the sample standard deviation was 20 minutes. Assume that the battery time distribution as normal.

a) Test if the average battery time is shorter than 4 hours at a = 0.05.

b) Construct a 95% confidence interval of the mean battery time.

c) If you were to test H0: µ =240 minutes vs. H1: µ ≠ 240 minutes, what would you conclude from your result in part (b)?

d) Suppose that a further study establishes that, in fact, e population mean is 4 hours. Did the test in part (c) make a correct decision? If not, what type of error did it make?7. A computer company claims that the batteries in its laptops last 4 hours on average. A consumer report firm gathered a sample of 16 batteries and conducted tests on this claim. The sample mean was 3 hours 50 minutes, and the sample standard deviation was 20 minutes. Assume that the battery time distribution as normal.

Answer 1

A. The average battery time is shorter than 4 hours at 0.05 level of significance and 15 degrees of freedom

B. The mean battery time is likely to be between 219.35 and 240.65 minutes at 95% confidence interval.

C. The average batter time is equal to 4 hours at 0.05 level of significance and 1 degrees of freedom

D. The test in part C made a correct decision

Step-by-step explanation: Please find the attached document for the step by step working and explanation

Answer 2

a) We can reject the null hypothesis and conclude that average battery time is shorter than 4 hours at a = 0.05

b) 95% confidence interval of the mean battery time is 230±11.55. That is between 218.45 min and 241.55 min.

c) If you were to test H0: µ =240 minutes vs. H1: µ ≠ 240 minutes, we can conclude that we fail to reject the null hypothesis, because confidence interval includes 240 min.

d) We made a correct decision at c, if study establishes that in fact, a population mean is 4 hours.

Explanation:

a)

H0: µ=240

H1: µ<240

Test statistic can be found using the equation

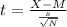`t=(X-M)/((s)/(√(N) ) )` where

• X = 230 min. (3 hours 50 minutes)

• M is the lasting time of laptop batteries claimed in null hypothesis (240 min.)

• s is the sample standard deviation (20 minutes)

• N is the sample size (16)

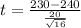`t=(230-240)/((20)/(√(16) ) )` = -2

One tailed p-value of t=-2 for 15 degrees of freedom is ≈ 0.032

Since 0.032<0.05, the result is significant. We can reject the null hypothesis and conclude that average battery time is shorter than 4 hours at a = 0.05

b) 95% confidence interval of the mean battery time can be calculated using M±
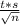`(t*s)/(√(n))`where

• M is the sample average lasting time (230 min)

• t is the two tailed statistic for 95% confidence level and 15 degrees of freedom (2.13)

• s is the sample standard deviation (20 min.)

• n is sample size (16)

230±
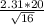`(2.31*20)/(√(16))` that is 230±11.55

c) If you were to test H0: µ =240 minutes vs. H1: µ ≠ 240 minutes, from 95% confidence interval which is between 218.45 min and 241.55 min, we can conclude that we fail to reject the null hypothesis, because confidence interval includes 240 min.

d) We made a correct decision at c, if study establishes that in fact, a population mean is 4 hours.