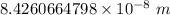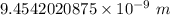Question

Suppose that the sound level of a conversation is initially at an angry 72 dB and then drops to a soothing 53 dB. Assuming that the frequency of the sound is 522 Hz, determine the (a) initial and (b) final sound intensities and the (c) initial and (d) final sound wave amplitudes. Assume the speed of sound is 343 m/s and the air density is 1.21 kg/m3.

Answer 1

`10^(-4.8)\ W/m^2`

`10^(-6.7)\ W/m^2`

`8.4260664798* 10^(-8)\ m`

`9.4542020875* 10^(-9)\ m`

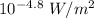
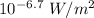
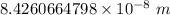
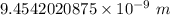
Step-by-step explanation:

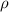`\rho` = Density of air = 1.21 kg/m³

v = Speed of sound in air = 343 m/s

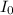`I_0` = Threshold intensity =
`10^(-12)\ W/m^2`

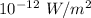
f = Frequency = 522 Hz

Intensity of sound is given by

`\beta=10log(I)/(I_0)\\\Rightarrow 72=10log(I)/(10^(-12))\\\Rightarrow (72)/(10)=log(I)/(10^(-12))\\\Rightarrow 10^{(72)/(10)}=(I)/(10^(-12))\\\Rightarrow I=10^{(72)/(10)}* 10^(-12)\\\Rightarrow I=10^(-4.8)\ W/m^2`

`\beta=10log(I)/(I_0)\\\Rightarrow 53=10log(I)/(10^(-12))\\\Rightarrow (53)/(10)=log(I)/(10^(-12))\\\Rightarrow 10^{(53)/(10)}=(I)/(10^(-12))\\\Rightarrow I=10^{(53)/(10)}* 10^(-12)\\\Rightarrow I=10^(-6.7)\ W/m^2`

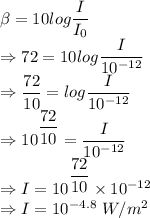
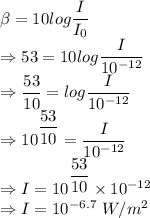
The intensities are

`10^(-4.8)\ W/m^2`

`10^(-6.7)\ W/m^2`

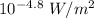
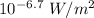
Intensity of sound is also given by

`I=2\pi^2\rho vf^2S^2\\\Rightarrow S=\sqrt{(I)/(2\pi^2\rho vf^2)}\\\Rightarrow S=\sqrt{(10^(-4.8))/(2\pi^2* 1.21* 343* 522^2)}\\\Rightarrow S=8.4260664798* 10^(-8)\ m`

`S=\sqrt{(I)/(2\pi^2\rho vf^2)}\\\Rightarrow S=\sqrt{(10^(-6.7))/(2\pi^2* 1.21* 343* 522^2)}\\\Rightarrow S=9.4542020875* 10^(-9)\ m`

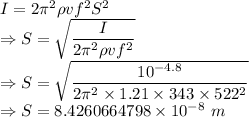
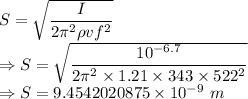
The amplitudes are

`8.4260664798* 10^(-8)\ m`

`9.4542020875* 10^(-9)\ m`