Question

A 10-cm-long thin glass rod uniformly charged to 11.0 nCnC and a 10-cm-long thin plastic rod uniformly charged to - 11.0 nCnC are placed side by side, 3.60 cmcm apart. What is the electric field strength 2.60 cmcm from the glass rod along the line connecting the midpoints of the two rods?

Answer 1

`\vec{E} = -1.27* 10^5~(\^x) ~N/C`

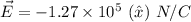
Step-by-step explanation:

We will find the E-fields created by the rods separately. The E-field is asked where the line connecting the midpoints of two rods, so we will look for the E-field at a distance 2.6 cm from the center of the rods.

For simplicity, I will define Q = 11.0 nC, and L = 0.1 m.

We will use the electric field formula:

`\vec{E} = (1)/(4\pi \epsilon_0)(Q)/(r^2)\^r`

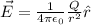
However, this formula is for point charges only. If you have a charge distribution, then you have to choose an infinitesimal portion of the rod, apply the formula for this portion, then integrate it over the whole rod.

We choose an infinitesimal portion with length 'dy' with a distance 'y' from the center of the rod. Here I assume that the rods are positioned on the y-axis.

The electric field for the infinitesimal portion is 'dE' and can be written as

`dE = (1)/(4\pi\epsilon_0)(dq)/(x^2 + y^2)`

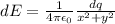
where dq is the charge of the small portion and x = 2.6 cm.

dq can be written in terms of the charge and length of the rod:

`(Q)/(L) = (dq)/(dy)\\dq = (Qdy)/(L)`

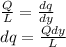
Let's plug this into dE:

`dE = (1)/(4\pi\epsilon_0)(Qdy)/(L(x^2+y^2))`

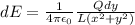
Since the E-field is a vector, dE is also a vector directed from dy to x. The next step in our method is to integrate dE over the boundaries of the rod, but we need to separate the x- and y-components of dE first, then we will integrate x and y components separately.

`dE_x = dE\cos(\theta)\\dE_y = dE\sin(\theta)`

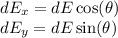
where θ is the angle between x-axis and dE. This angle can be found by the triangle formed by three points: x, dy, and the origin.

`\sin(\theta) = (y)/(√(x^2+y^2))\\\cos(\theta) = (x)/(√(x^2+y^2))`

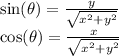
Therefore, the x- and y-components of dE can be found:

`dE_x = (1)/(4\pi\epsilon_0)(Qxdy)/(L(x^2+y^2)^(3/2))\\dE_y = (1)/(4\pi\epsilon_0)(Qydy)/(L(x^2+y^2)^(3/2))`

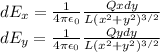
Finally, we can integrate these results over the entire rod to find the total E-field.

`E_x = \int\limits^(L/2)_(-L/2) {dE_x} \, dy = (Qx)/(4\pi\epsilon_0 L)\int\limits^(L/2)_(-L/2) {(1)/((x^2+y^2)^(3/2))} \, dx = (Qx)/(4\pi\epsilon_0 L)(2L)/(x^2√(4x^2+L^2)) = (Q)/(2\pi\epsilon_0x√(4x^2+L^2))`

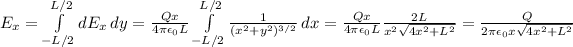
Substituting Q, L and x gives the final result:

`E_x = 6.78* 10^4 N/C`

in the direction of +x.

The integral for the y-component gives

`E_y = (Q)/(4\pi\epsilon_0 L)\int\limits^(L/2)_(-L/2) {(y)/((x^2+y^2)^(3/2))} \, dy = 0`

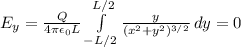
This actually makes sense, because we are looking for the E-field at y = 0. The upper part creates an E-field, and the lower part creates the same E-field but in the opposite direction. So they cancel out each other in the end.

As for the plastic rod, the same equations applies. To avoid repetition, the results from the glass rod can be used.

This time, Q = -11 nC and x = 1 cm.

`E_x = -1.95 * 10^5~N/C`

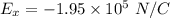
in the direction of -x.

The y-component of E-field is again zero due to the symmetry.

Finally, we can add the two E-field vectors and find the resulting field.

`\vec{E} = 6.78 * 10^4~\^x - 1.95 * 10^5~\^x\\\vec{E} = -1.27 * 10^5~\^x`