Answer:
0.176 m/s
Step-by-step explanation:
given,
mass of the puck, m = 170 g
Length of the ramp, L = 3.6 mm
angle of inclination, θ = 26°
the minimum speed require to reach at the top of the ramp
using equation of motion
v² = u² + 2 a s
final speed of the puck is zero
0² = u² - 2 g s

height of the pluck
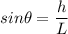
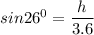
h = 1.58 mm
h = 0.00158 m
now,

u = 0.176 m/s
hence, the speed required by the pluck to reach at the top is equal to 0.176 m/s