Question

A solid sphere, solid cylinder, and a hollow pipe all have equal masses and radii and are of uniform density. If the three are released simultaneously at the top of an inclined plane and roll without slipping which one will reach the bottom first? a. solid sphere b. solid cylinder c. hollow pipe d. They all reach the bottom at the time.

Answer 1

b. solid cylinder

Step-by-step explanation:

m = Mass of object

`\theta` = Angle of slope

I = Moment of inertia

r = Radius

g = Acceleration due to gravity = 9.81 m/s²

The acceleration of an object rolling down a slope is given by

`a=(mgsin\theta)/(m+(I)/(r^2))`

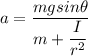
Now the time taken will be less if the acceleration is higher.

It can be seen that the acceleration is inversely proportional to the moment of inertia.

So, the moment of inertia which is least will give the maximum acceleration

For solid sphere

`I=(2)/(5)mr^2`

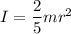
For solid cylinder

`I=(1)/(2)mr^2`

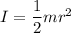
For hollow pipe

`I=mr^2`

So, the solid sphere will have the lowest moment of inertia implying highest acceleration.

Hence, the solid sphere will reach the bottom first.