Answer: a) 0.01884167 b) 0.00017858 c) 5
Explanation:
Given : The proportion of Californians own a car = 0.66
Sample size : n=8
We assume that each Californian is independent from other.
Let x be the number of Californians own a car.
Then, X
 Bin (n=8 , p=0.66)
Bin (n=8 , p=0.66)
Binomial probability formula =
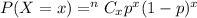
, where p=probability of getting success in each trial.
a) The probability that two of them own a car =
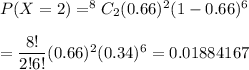
∴ The probability that two of them own a car is 0.01884167.
(b) The probability at least one of the owns a car =
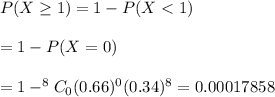
∴ The probability at least one of the owns a car is 0.00017858.
(c) The expected number of Californians own a car =

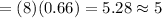
Hence, the expected number of Californians own a car = 5