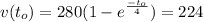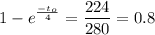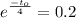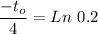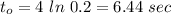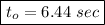Question

Suppose that the acceleration of a model rocket is proportional to the difference between 280 ft/sec and the rocket's velocity. If it is initially at rest and its initial acceleration is 70 ft/sec2, how long will it take to accelerate to 224 ft/s?

Answer 1

to=6.44 sec

Step-by-step explanation:

Differential Equations In Physics

Most definitions in physics come in form of differential equations. Accelerated motion is a common example where the instant value of the magnitudes is proportional to the derivative of others.

The acceleration is defined as the rate of change of the velocity

`\displaystyle a=(dv)/(dt)`

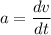
if we know the relation between them, then we can solve the resulting differential equation like shown below. The question tells us the acceleration and the velocity are related through the following equation

`\displaystyle a=k(280-v)`

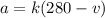
Using the above definition, we have a differential equation.

`\displaystyle (dv)/(dt)=k(280-v)`

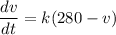
It can be easily solved because the variables can be separated

`\displaystyle (dv)/(280-v)=k\ dt`

`\displaystyle (dv)/(v-280)=-k\ dt`

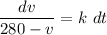
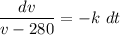
Integrating both sides

`\displaystyle \int (dv)/(v-280)=\int -k\ dt`

`\displaystyle Ln|v-280|=-k\ t+d`

`\displaystyle v-280=c\ e^(-kt)`

`\displaystyle v=280+c\ e^(-k\ t)`

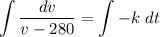
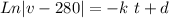
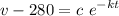
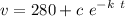
This is the general equation of the velocity, we need to find the value of k and C. The initial conditions set v(0)=0, thus

`\displaystyle v(0)=0=280+c`

`\displaystyle c=-280`

`\displaystyle v(t)=280(1-e^(-k\ t))`

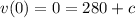
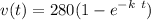
To compute the value of k, we need to find the equation of the acceleration by taking the derivative of v

`\displaystyle a=(dv)/(dt)=280\ k\ e^(-k\ t)`

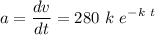
The other condition sets the initial acceleration =
`70 ft/s^2`

`\displaystyle a(0)=70=280\ k`

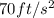
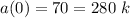
We find the value of k

`\displaystyle k=(1)/(4)`

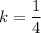
The equation of the acceleration is

`\displaystyle a(t)=280((1)/(4))e^{(-t)/(4)}`

`\displaystyle a(t)=70\ e^{(-t)/(4)}`

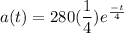
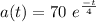
And the equation of the velocity is

`\displaystyle v(t)=280(1-e^(-t)/(4))`

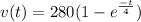
We need to find the time t0 at which the velocity is 224 ft/s, thus

`\displaystyle v(t_o)=280(1-e^(-t_o)/(4))=224`

`\displaystyle 1-e^(-t_o)/(4)=(224)/(280)=0.8`

`\displaystyle e^(-t_o)/(4)=0.2`

`\displaystyle (-t_o)/(4)=Ln\ 0.2`

`\displaystyle t_o=4\ ln\ 0.2=6.44\ sec`

`\boxed{\displaystyle t_o=6.44\ sec}`