Question

Below are the jersey numbers of 11 players randomly selected from a football team. Find the range, variance, and standard deviation for the given sample data. What do the results tell us? 33 29 97 56 26 78 83 74 65 47 58 Range = (Round to one decimal place as needed.) Sample standard deviations ? = (Round to one decimal place as needed) Sample variance = (Round to one decimal place as needed) What do the results tell us? a. Jersey numbers are nominal data that are just replacements for names, so the resulting statistics are meaningless. b. Jersey numbers on a football team vary much more than expected c. The sample standard deviation is too large in comparison to the range. d. Jersey numbers on a football team do not vary as much as expected.

Answer 1

Range = 71

Variance = 546.0

Standard Deviation = 23.4

Option A) Jersey numbers are nominal data that are just replacements for names, so the resulting statistics are meaningless.

Explanation:

We are given the following data set in the question:

33, 29, 97, 56, 26, 78, 83, 74, 65, 47, 58

Formula:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

`\text{Variance} = \displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}`

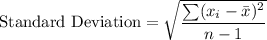
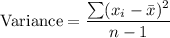
where
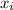`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(646)/(11) = 58.7`

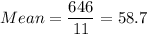
Sum of squares of differences = 5460.18

`\text{Variance} = (5460.18)/(11) = 546.0`

`S.D = \sqrt{(5460.18)/(10)} = 23.4`

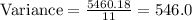
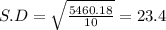
Sorted Data Set: 26, 29, 33, 47, 56, 58, 65, 74, 78, 83, 97

Range = Maximum - Minimum

Range = 97 - 26 = 71

Based on the values, we can say that

Option A) Jersey numbers are nominal data that are just replacements for names, so the resulting statistics are meaningless.