Question

Calculate the average linear momentum of a particle described by the following wavefunctions: (a) eikx, (b) cos kx, (c) e−ax2 , where in each one x ranges from −[infinity] to +[infinity].

Answer 1

a) p=0, b) p=0, c) p= ∞

Step-by-step explanation:

In quantum mechanics the moment operator is given by

p = - i h’ d φ / dx

h’= h / 2π

We apply this equation to the given wave functions

a) φ =
`e^(ikx)`

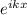
.d φ dx = i k
`e^(ikx)`

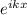
We replace

p = h’ k
`e^(ikx)`

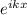
i i = -1

The exponential is a sine and cosine function, so its measured value is zero, so the average moment is zero

p = 0

b) φ = cos kx

p = h’ k sen kx

The average sine function is zero,

p = 0

c) φ =
`e^{-ax^(2) }`

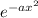
d φ / dx = -a 2x
`e^{-ax^(2) }`

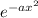
.p = i a g ’2x
`e^{-ax^(2) }`

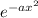
The average moment is

p = (p₂ + p₁) / 2

p = i a h ’(-∞ + ∞)

p = ∞