This is an incomplete question, here is a complete question.
The heat of combustion of bituminous coal is 2.50 × 10² J/g. What quantity of the coal is required to produce the energy to convert 106.9 pounds of ice at 0.00 °C to steam at 100 °C?
Specific heat (ice) = 2.10 J/g°C
Specific heat (water) = 4.18 J/g°C
Heat of fusion = 333 J/g
Heat of vaporization = 2258 J/g
A) 5.84 kg
B) 0.646 kg
C) 0.811 kg
D) 4.38 kg
E) 1.46 kg
Answer : The correct option is, (A) 5.84 kg
Explanation :
The process involved in this problem are :

The expression used will be:
![Q=[m* \Delta H_(fusion)]+[m* c_(p,l)* (T_(final)-T_(initial))]+[m* \Delta H_(vap)]](https://img.qammunity.org/2021/formulas/chemistry/college/7o3h4y4n2nrtzwoauhemyacqphsrtt8jtp.png)
where,
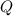 = heat required for the reaction = ?
= heat required for the reaction = ?
m = mass of ice = 106.9 lb = 48489.024 g (1 lb = 453.592 g)
 = specific heat of liquid water =
= specific heat of liquid water =
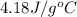
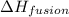 = enthalpy change for fusion =
= enthalpy change for fusion =
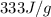
 = enthalpy change for vaporization =
= enthalpy change for vaporization =
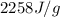
Now put all the given values in the above expression, we get:
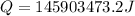
Now we have to calculate the quantity of the coal required.
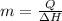

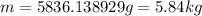 (1 g = 0.001 kg)
(1 g = 0.001 kg)
Thus, the quantity of the coal required is, 5.84 kg