Question

The sum of four consecutive even integers is 28

Answer 1

The four consecutive even integers are 4, 6, 8 and 10.

Explanation:

Let the four consecutive even integers be
`x, x+2, x+4, x+6`

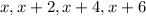
It is provided that the sum of these consecutive even integers is 28.

Solve for x as follows:

`x+ x+2+ x+4+ x+6=28\\4x+12=28\\4x=16\\x=4`

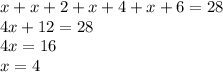
The four consecutive even integers are:

`x=4\\x+2=4+2=6\\x+4 = 4 +4 =8\\x+6=4+6=10`

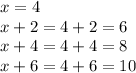
Thus, the four consecutive even integers are 4, 6, 8 and 10.