Question

A river flows due south with a speed of 2.10 m/s. A man steers a motorboat across the river; his velocity relative to the water is 4.50 m/s. The river is 600 m wide.

1. In what direction should the motorboat head in order to reach a point on the opposite bank directly east from the starting point? (The boat's speed relative to the water remains 4.50) answer needs to be in degrees north of east.

2. What is the velocity of the boat relative to the earth? m/s is the units (the book says the answer is 3.98 m/s

3. How much time is required to cross the river? s (sec) is the units ( the book says the answer is 151 s)

Answer 1

1. 27.8 degree north of east

2. 3.98 m/s

3. 151 s

Step-by-step explanation:

1. For the boat to reach a point on the opposite bank directly east from the starting point, its vertical velocity component must be the same but in opposite direction with the river vertical velocity of 2.1 m/s. The 2 velocities would cancel each other so the boat has 0 vertical velocity relative to Earth.

The direction, relative to east is,

`sin(\alpha) = 2.1/4.5 = 0.467`

`\alpha = sin^(-1)(0.467) = 0.486 rad = 0.486*180/\pi = 27.8^0`

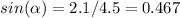
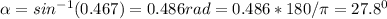
2. Since the vertical velocities cancels out, we only accounts for horizontal velocity

`v_h^2 + v_v^2 = v^2 = 4.5 ^2 = 20.25`

`v_h^2 + 2.1^2 = 20.25`

`v_h^2 = 20.25 - 4.41 = 15.84`

`v_h = √(15.84) = 3.98 m/s`

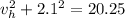
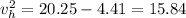
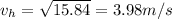
3. The time it takes to cross the 600m wide river at speed of 3.98 m/s, horizontally, is

t = 600 / 3.98 = 151 s