Question

3.Mr. Smith's class sold wrapping paper for $ 3.50 each and Mr. Davis ' class sold magazines for $2.75 each. Together, the classes sold 72 items and earned $222 for their school a Write and solve a system of equations that model the problemShow all your work b Which class earned more money ? How much more money did that class earn?

Answer 1

Mr. Smith's class sold 32 items for $112 and Mr. Davis's class sold 40 items for $110

Mr. Smith's class earned $2 more.

Explanation:

Let

x = number of items Mr. Smith's class sold

y = number of items Mr. Davis's class sold

1. Together, the classes sold 72 items, then

`x+y=72`

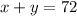
2. .Mr. Smith's class sold wrapping paper for $3.50 each, so x items cost $3.50x.

Mr. Davis ' class sold magazines for $2.75 each, so y items cost $2.75y.

Together, the classes earned $222, then

`3.5x+2.75y=222`

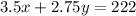
3. You get the system of two equations:

`\left\{\begin{array}{l}x+y=72\\ \\3.5x+2.75y=222\end{array}\right.`

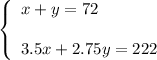
From the first equation,

`x=72-y,`

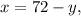
substitute it into the second equation:

`3.5(72-y)+2.75y=222\\ \\252-3.5y+2.75y=222\\ \\-3.5y+2.75y=222-252\\ \\-0.75y=-30\\ \\75y=3,000\\ \\y=40\\ \\x=72-y=72-40=32`

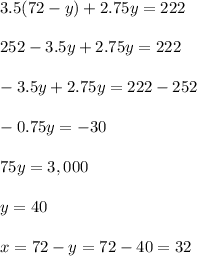
Mr. Smith's class sold 32 items for
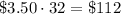`\$3.50\cdot 32=\$112` and Mr. Davis's class sold 40 items for
`\$2.75\cdot 40=\$110`

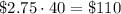
Mr. Smith's class earned
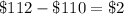`\$112-\$110=\$2` more.