Answer: 0.5
Explanation:
Given : Delta Airlines quotes a flight time of 2 hours, 5 minutes for its flights from Cincinnati to Tampa.
i.e. Flight time = 2(60) +5= 125 minutes [∵ 1 hour = 60 minutes]
Actual flight times are uniformly distributed between 2 hours and 2 hours, 20 minutes.
i.e. In minutes the flight times are between 120 minutes and 140 minutes.
Let x be a uniformly distributed variable in [120 minutes, 140 minutes] that represents the flight time.
Since the probability density function for x uniformly distributed in [a,b] is
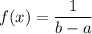
⇒ Probability density function for flight time :
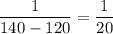
5 minutes late than usual time = Flight time+ 5 = 125+5 = 130 minutes
Now , the probability that the flight will be no more than 5 minutes late will be :-
![\int^(130)_(120) (1)/(20)\ dx\\\\=(1)/(20)[x]^(130)_(120)\\\\= (130-120)/(20)\\\\=(1)/(2)=0.5](https://img.qammunity.org/2021/formulas/mathematics/college/pyjgstj0sv3w6yhjqllzunzynpva1lau34.png)
Hence, the probability that the flight will be no more than 5 minutes late is 0.5.