➣Given
- ➣shipping carton basically shape is rectangular prism type
- ➣its volume (shipping carton)=72in²
- ➣its height =3in
- ➣its width = 4in
- ➣ assumption :- length "c"


★ Let's substitute values according to given info
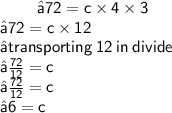

★ Hence "c" (length) of Rectangular prism (shipping carton) is
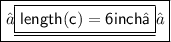
Hope it helps !