Answer:
-3.769 m/min
Step-by-step explanation:
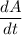 = Rate of change of area = -49 m²/min (negative due to shrinking)
= Rate of change of area = -49 m²/min (negative due to shrinking)
s = Side length = 13 m
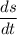 = Rate of change of side
= Rate of change of side
Area of a square is given by
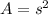
Differentiating with respect to time
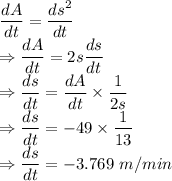
The rate of change of the sides of the square is -3.769 m/min