Answer:
- Volume of cone = 127.17 cm³
Explanation:
In the question we are given ,
And we are asked to find the volume of cone. We know that ,

Where ,
So , for finding volume of cone we must have to find the height of cone using slant height formula i.e. ,
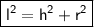
Where ,
Now , substituting values :
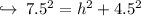
Transposing 4.5 to left hand side :


On further calculations we get :
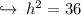
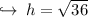
We know that 6 × 6 is equal to 36 that means square root of 36 is 6 . So :
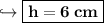
- Therefore, height of cylinder is 6 cm .
Now finding volume :
Substituting values in volume formula :
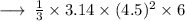
Step 1 : By cancelling 6 with 3 we get :

Step 2 : Multiplying 20.25 with 2 :
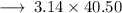
Step 3 : Multiplying 3.14 with 40.50 :
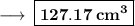
- Therefore, volume of cone is 127.17 cm³ .
#Keep Learning