Question

Tricia completed the square of the quadratic function f(x) = x² + 14x + 2 and determined the coordinates of the minimum value are (-7, - 47). Which equation must be Tricia's result?

f(x = (x +7)² + 47
f(x) = (x + 7)² - 47
f(x) = (x - 7)² + 47
f(x) = (x - 7)² - 47

Answer 1

The co-ordinates which give the minimum value for the quadratic function are (-7, -47)

Explanation:

i) the quadratic function f(x) =
`x^(2)` + 14x + 2

=
`x^(2)` + 14x + 49 - 49 + 2

=
`(x + 7)^(2)` - 49 + 2

=
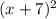`(x+7)^(2)` - 47

ii) The minimum value of the result of the quadratic equation in i) will be achieved when
`(x + 7)^(2)` is zero as any square value is always positive and thus the minimum value of a square is always zero.

iii)
`(x + 7)^(2)` is zero when x = -7 and when x = -7 then y = f(x) = -47

iv) The co-ordinates which give the minimum value for the quadratic function are (-7, -47)