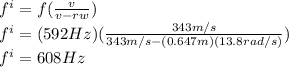Answer:
(a) lowest frequency=577 Hz
(b) highest frequency=608 Hz
Step-by-step explanation:
Given data
f(whistle frequency)=592 Hz
ω(angular speed)=13.8 rad/s
r(radius)=64.7 cm=0.647 m
To find
(a) Lowest frequency
(b) highest frequency
Solution
From Doppler effect
f=f×{(v±vd)/(v±vs)}
Where
v is speed of sound
Vd is speed detector relative to the medium(vd=0)
Vs is the speed of the source
Since
v=rω
For (a) lowest frequency
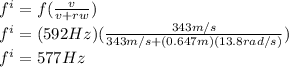
For (b) highest frequency