Question

A 20.0 mL sample of 0.200 M K₂CO₃ solution is added to 30.0 mL of 0.400 M Ba(NO₃)₂ solution. Barium carbonate precipitates.

The concentration of barium ion, Ba²⁺, in solution after the reaction is ______.

Answer 1

Answer: The concentration of barium ions is 0.08 M

Step-by-step explanation:

To calculate the number of moles for given molarity, we use the equation:

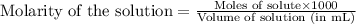`\text{Molarity of the solution}=\frac{\text{Moles of solute}* 1000}{\text{Volume of solution (in mL)}}` .....(1)

• For potassium carbonate:

Molarity of potassium carbonate = 0.200 M

Volume of solution = 20.0 mL

Putting values in equation 1, we get:

`0.200M=\frac{\text{Moles of potassium carbonate}* 1000}{20.0}\\\\\text{Moles of potassium carbonate}=((0.200* 20.0))/(1000)=0.004mol`

• For barium nitrate:

Molarity of barium nitrate = 0.400 M

Volume of solution = 30.0 mL

Putting values in equation 1, we get:

`0.400M=\frac{\text{Moles of barium nitrate}* 1000}{30.0}\\\\\text{Moles of barium nitrate}=((0.400* 30.0))/(1000)=0.012mol`

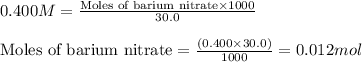
The chemical equation for the reaction of potassium carbonate and barium nitrate follows:

`K_2CO_3(aq.)+Ba(NO_3)_2(aq.)\rightarrow BaCO_3(s)+2KNO_3(aq.)`

By Stoichiometry of the reaction:

1 mole of potassium carbonate reacts with 1 mole of barium nitrate

So, 0.004 moles of potassium carbonate will react with =
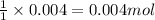`(1)/(1)* 0.004=0.004mol` of barium nitrate

As, given amount of barium nitrate is more than the required amount. So, it is considered as an excess reagent.

Thus, potassium carbonate is considered as a limiting reagent because it limits the formation of product.

By Stoichiometry of the reaction:

1 mole of potassium carbonate produces 1 mole of barium carbonate

So, 0.004 moles of potassium carbonate will produce =
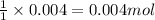`(1)/(1)* 0.004=0.004mol` of barium carbonate

We know that:

1 mole of barium carbonate produces 1 mole of barium ions and 1 mole of carbonate ions

Moles of barium ions = 0.004 moles

Volume of solution = (20 + 30) mL = 50 mL

Putting values in equation 1, we get:

`\text{Concentration of }Ba^(2+)\text{ ions}=(0.004* 1000)/(50)\\\\\text{Concentration of }Ba^(2+)\text{ ions}=0.08M`

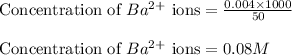
Hence, the concentration of barium ions is 0.08 M