Question

Find the exact value of cos theta​, given that sin thetaequalsStartFraction 15 Over 17 EndFraction and theta is in quadrant II. Rationalize denominators when applicable.

Answer 1

It is D

Explanation:

EDGE 2021

Answer 2

`cos \theta = -(8)/(17)`

Explanation:

For this case we know that:

`sin \theta = (15)/(17)`

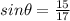
And we want to find the value for
`cos \theta`, so then we can use the following basic identity:

`cos^2 \theta + sin^2 \theta =1`

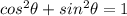
And if we solve for
`cos \theta` we got:

`cos^2 \theta = 1- sin^2 \theta`

`cos \theta =\pm √(1-sin^2 \theta)`

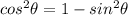
And if we replace the value given we got:

`cos \theta =\pm \sqrt{1- ((15)/(17))^2}=\sqrt{(64)/(289)}=(√(64))/(√(289))=(8)/(17)`

For our case we know that the angle is on the II quadrant, and on this quadrant we know that the sine is positive but the cosine is negative so then the correct answer for this case would be:

`cos \theta = -(8)/(17)`