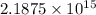Question

A cyclotron is used to produce a beam of high-energy deuterons that then collide with a target to produce radioactive isotopes for a medical procedure. Deuterons are nuclei of deuterium, an isotope of hydrogen, consisting of one neutron and one proton, with total mass 3.34×10−27kg. The deuterons exit the cyclotron with a kinetic energy of 3.80 MeV.

a. What is the speed of the deuterons when they exit?
b. If the magnetic field inside the cyclotron is 1.25 T, what is the diameter of the deuterons' largest orbit, just before they exit?
c. If the beam current is 350 μA how many deuterons strike the target each second?

Answer 1

19080667.0818 m/s

0.637294 m

`2.1875* 10^(15)`

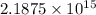
Step-by-step explanation:

m = Mass of deuterons =
`3.34* 10^(-27)\ kg`

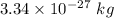
v = Velocity

K = Kinetic energy = 3.8 MeV

d = Diameter

B = Magnetic field = 1.25 T

q = Charge of electron =
`1.6* 10^(-19)\ C`

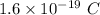
t = Time = 1 s

i = Current = 350 μA

Kinetic energy is given by

`K=(1)/(2)mv^2\\\Rightarrow v=\sqrt{(2K)/(m)}\\\Rightarrow v=\sqrt{(2* 3.8* 10^6* 1.6* 10^(-19))/(3.34* 10^(-27))}\\\Rightarrow v=19080667.0818\ m/s`

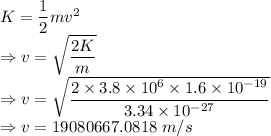
The speed of the deuterons when they exit is 19080667.0818 m/s

In this system the centripetal and magnetic force will balance each other

`(mv^2)/(r)=qvB\\\Rightarrow (mv^2)/((d)/(2))=qvB\\\Rightarrow d=(2mv)/(qB)\\\Rightarrow d=(2* 3.34* 10^(-27)* 19080667.0818)/(1.6* 10^(-19)* 1.25)\\\Rightarrow d=0.637294\ m`

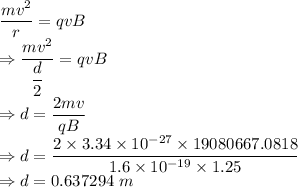
The diameter is 0.637294 m

Current is given by

`i=(nq)/(t)\\\Rightarrow n=(it)/(q)\\\Rightarrow n=(350* 10^(-6)* 1)/(1.6* 10^(-19))\\\Rightarrow n=2.1875* 10^(15)`

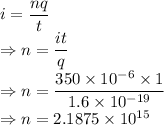
The number of deuterons is
`2.1875* 10^(15)`