Answer:
For 1: The value of
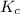 is 10.24
is 10.24
For 2: The value of
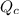 is 9.07
is 9.07
For 3: The new equilibrium concentration of A is 0.220 M
Step-by-step explanation:
We are given:
Volume of the container = 2.00 L
Equilibrium moles of A = 0.50 moles
Equilibrium moles of B = 0.50 moles
Equilibrium moles of C = 1.60 moles
Equilibrium moles of D = 1.60 moles
We know that:
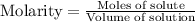
For the given chemical reaction:
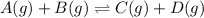
The expression of
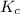 for above equation follows:
for above equation follows:
![K_c=([C][D])/([A][B])](https://img.qammunity.org/2021/formulas/chemistry/college/z9ueyj7kd0gl56tvwtllmyg483rvar0w1k.png)
We are given:
![[A]_(eq)=(0.50)/(2.00)=0.25](https://img.qammunity.org/2021/formulas/chemistry/college/ntzpvclbydsc9hvmv4o1voh3j2cyi8nsav.png)
![[B]_(eq)=(0.50)/(2.00)=0.25](https://img.qammunity.org/2021/formulas/chemistry/college/ivrqofmwdbj2hh2el2bnwkom0t6pmpublu.png)
![[C]_(eq)=(1.60)/(2.00)=0.8](https://img.qammunity.org/2021/formulas/chemistry/college/kn6q6whj9ajtr1v9fhtz7uv2dhaoyyrndq.png)
![[D]_(eq)=(1.60)/(2.00)=0.8](https://img.qammunity.org/2021/formulas/chemistry/college/se0iqdm7jg0ck16dur2a215ttlxd1kh6ln.png)
Putting values in above equation, we get:
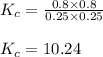
Hence, the value of
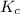 is 10.24
is 10.24
Added moles of B = 0.10 moles
Added moles of C = 0.10 moles
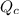 is the quotient of activities of products and reactants at any stage other than equilibrium of a reaction.
is the quotient of activities of products and reactants at any stage other than equilibrium of a reaction.
![Q_c=([C][D])/([A][B])](https://img.qammunity.org/2021/formulas/chemistry/college/fj9sd0omkh1ncl18o00h0p74doucvpwi8t.png)
Now,
![[A]=(0.50)/(2.00)=0.25](https://img.qammunity.org/2021/formulas/chemistry/college/wd3c9bi28nlf3re3cbizzyd7skgudknfqz.png)
![[B]=(0.60)/(2.00)=0.3](https://img.qammunity.org/2021/formulas/chemistry/college/p41dhunl9mwabvwd0s8wjqtcw2wn8uz9iq.png)
![[C]=(1.70)/(2.00)=0.85](https://img.qammunity.org/2021/formulas/chemistry/college/afkhztqx0zg89in8ko0maxgneuz4ip3umr.png)
![[D]=(1.60)/(2.00)=0.8](https://img.qammunity.org/2021/formulas/chemistry/college/zhuzjxs0j17gbpzl57n10vobunoui8wb7g.png)
Putting values in above equation, we get:

Hence, the value of
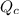 is 9.07
is 9.07
Taking equilibrium constant as 10.24 for calculating the equilibrium concentration of A.
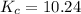
![[B]_(eq)=(0.60)/(2.00)=0.3](https://img.qammunity.org/2021/formulas/chemistry/college/9d4no834zvzwm9kx1bjygnc1it4s2ogohr.png)
![[C]_(eq)=(1.70)/(2.00)=0.85](https://img.qammunity.org/2021/formulas/chemistry/college/l4oqdcj1fwgy2n76h6dpkm9pln72swrh5j.png)
![[D]_(eq)=(1.60)/(2.00)=0.8](https://img.qammunity.org/2021/formulas/chemistry/college/se0iqdm7jg0ck16dur2a215ttlxd1kh6ln.png)
Putting values in expression 1, we get:
![10.24=(0.85* 0.8)/([A]* 0.3)](https://img.qammunity.org/2021/formulas/chemistry/college/3oge76o9qfnipa6h4kla2wk804ruiavtf2.png)
![[A]_(eq)=(0.85* 0.8)/(0.3* 10.24)=0.220](https://img.qammunity.org/2021/formulas/chemistry/college/gbdd6yaszypm9a7cmh43p541vaxso5jdlk.png)
Hence, the new equilibrium concentration of A is 0.220 M