Question

The equation A(t) = 900(0.85)t represents the value of a motor scooter t years after it was purchased. Which statements are also true of this situation?

Answer 1

When new, the scooter cost $900

Explanation:

The complete question in the attached figure

we have

`A(t)=900(0.85)^t`

This is a exponential function of the form

`A(t)=a(b)^t`

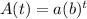
where

A(t) ----> represent the value of a motor scooter

t ----> the number of years after it was purchased

a ---> represent the initial value or y-intercept

b is the base of the exponential function

r is the percent rate of change

b=(1+r)

In this problem we have

`a=\$900\\b=0.85`

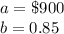
The base b is less than 1

That means ----> is a exponential decay function (is a decreasing function)

Find the percent rate of change

`b=(1+r)\\0.85=1+r\\r=0.85-1\\r=-0.15`

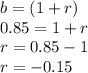
Convert to percentage (multiply by 100)

`r=-15\%` ---> negative means is a decreasing function

Verify each statements

case A) When new, the scooter cost $765.

The statement is false

Because the original value of the scooter was $900

case B) When new, the scooter cost $900

The statement is true (see the explanation)

case C) The scooter’s value is decreasing at a rate of 85% each year

The statement is false

Because the scooter’s value is decreasing at a rate of 15% each year (see the explanation)

case D) The scooter’s value is decreasing at a rate of 0.15% each year

The statement is false

Because the scooter’s value is decreasing at a rate of 15% each year (see the explanation)