Answer:
This is useful to choose which calculation to perform.
Explanation:
1) Firstly, let's consider that the Binomial Distribution tends to the Poisson Distribution given certain conditions:

Roughly, they tend to the same value.
2) The Binomial Probability is calculated through this formula:
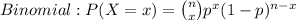
Poisson Distribution this way:
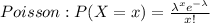
3) If we plug
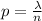
In the Binomial formula, given an "n" a very large quantity we'll have a closer outcome to Poisson.
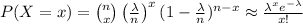
4) This is useful especially due to the convenience of calculating.
Because operating with exponentials and factorials, is hard and sometimes 'n' and 'p' may also be unknown, and sometimes the known parameter is the Mean.