Question

ASAP! I NEED THIS DONE AS QUICKLY AS POSSIBLE WITH WORKING OUT

After t seconds, a particle P has position vector
r = [(3t³- t + 3)i + (2t²+ 2t - 1)j] m
(a) Find an expression for the velocity of P in terms of t
(b) Find an expression for the acceleration of P in terms of t

Answer 1

See explanation.

Explanation:

Let us first analyze some principle theory. By definition we know that the velocity (
`v` ) is a function of a distance (
`d` ) covered in some time (
`t` ), whilst acceleration (
`a` ) is the velocity achieved in some time. These can also been expressed as:

`v = (d)/(t)\\` and
`a=(v)/(t)`

We also know that both velocity and acceleration are vectors (therefore they are characterized by both a magnitude and a direction). Finally we know that given a position vector we can find the velocity and the acceleration, by differentiating the vector with respect to time, once and twice, respectively.

Let us now solve our problem. Here we are givine the Position vector of a particle P (in two dimensional space of
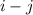`i-j` ) as:

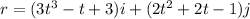`r=(3t^3-t+3)i+(2t^2+2t-1)j` Eqn.(1)

Let us solve.

Part (a) Velocity: we need to differentiate Eqn.(1) with respect to time as:

`v(t)=(dr)/(dt)\\\\ v(t)=[(3)3t^2-1]i+[(2)2t+2]j\\\\v(t)=(9t^2-1)i+(4t+2)j` Eqn.(2)

Part (b) Acceleration: we need to differentiate Eqn.(2) with respect to time as:

`a(t)=(dv)/(dt)\\ \\a(t)=[(2)9t]i+4j\\\\a(t)=(18t)i+4j`

Thus the expressions for the velocity and the acceleration of particle P in terms of t are

`v(t)=(9t^2-1)i+(4t+2)j` and
`a(t)=(18t)i+4j`