Answer:
The first space is 3,
The second space is -2
The third space is 100
Explanation:
A circle with center (a, b) and has radius r has equation:
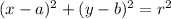
Now, if the circle passes through (-3, 2) and it has center on (5, -4). That means the radius of the circle will be the distance between points (-3, 2) and (5, -4).
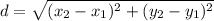
where d = formula of distance between points
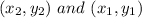
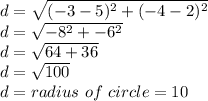
Now, with r = 10, a = -3, b = 2
The equation of circle becomes:

The first space is 3,
The second space is -2
The third space is 100