Question

The probability of a radar station detecting an enemy plane is 0.85 and the probability of not detecting an enemy plane is 0.15. If 4 stations are in use, what is the standard deviation? Round your answer to nearest hundredth.

Answer 1

The standard deviation is of 0.71 enemies planes detected.

Explanation:

For example enemy plane, there are only two possible outcomes. Either it is detected, or it is not. So we use the binomial probability distribution to solve this problem.

The standard deviation of n trials with probability p, of the binomial probability distribution, is given by the following formula.

`√(V(X)) = √(np(1-p)))`

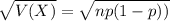
In this problem, we have that:

`p = 0.85, n = 4`

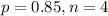
So

`√(V(X)) = √(np(1-p))) = √(4*0.85*0.15) = 0.71`

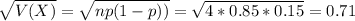
The standard deviation is of 0.71 enemies planes detected.