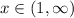Question

Y = 1/(x² + c)

is a one-parameter family of solutions of the first-order DE y' + 2xy² = 0.
Find a solution of the first-order IVP consisting of this differential equation and the given initial condition. Give the largest interval I over which the solution is defined.

Answer 1

`y(x)=(1)/(x^2-1)`

`x\in (1,\infty)`

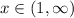
Explanation:

We are given that one parameter family of solution of the first order DE

`y=(1)/(x^2+c)`

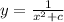
DE

`y'+2xy^2=0`

`y(2)=(1)/(3)`

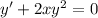
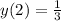
Substitute x=2

`(1)/(3)=(1)/(2^2+c)`

`(1)/(3)=(1)/(4+c)`

`4+c=3`

`c=3-4=-1`

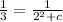
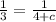
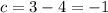
Substitute the value of c

`y(x)=(1)/(x^2-1)`

Solution is defined for all values of x except x=
`\pm 1`

Therefore, by unique existence theorem

The largest interval on which the solution is defined

`x\in (1,\infty)`