Answer:
Step-by-step explanation:
We will use x and y as our positive numbers. We need to write 2 equations from this information. The first is that the difference between the numbers is 7:
x - y = 7 is the equation for that.
The second is that the product of the 2 numbers is 294:
xy = 294
Let's begin by solving the first equation for x:
x = 7 + y
Now sub that in for x in the second equation:
(7 + y)y = 294 and
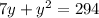
This is a quadratic, so let's put it into standard form, setting it equal to 0:

We have to factor this now to find out what values of y satisfy this equation.
Think: "what 2 number multiply to equal -294 and add to equal 7. To find these numbers we find all the factors of 294, which are:
1, 294
2, 147
3, 98
6, 49
7, 42
14, 21
It looks like 14 and 21 will work. If we make the 14 negative, then 21 - 14 = 7. And if the 14 is negative, then -14 * 21 = -294. So the signs are correct. The equation rewritten using those values in place of 7y is:
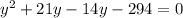 and we factor by grouping:
and we factor by grouping:
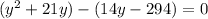
Out of the first set of parenthesis we can pull out a y, and from the second set we can pull out a 14:
y(y + 21) - 14(y + 21) = 0
What's common now is the factor (y + 21). So factor THAT out, and you're left with:
(y + 21)(y - 14) = 0
Set each of these expression equal to 0 and solve for y:
y + 21 = 0 so
y = -21 and
y - 14 = 0 so
y = 14
Since we were told that both of the numbers are positive, then y has to be 14.
Sub in y = 14 to find x:
x = 7 + 14 so
x = 21
There you go!