To solve this problem we will apply the concepts related to linear expansion in bodies when there is a temperature difference. For this case, this linear relationship is given by the function,
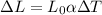
Here,
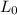 = Initial Length
= Initial Length
 = Coefficient of linear expansion of steel
= Coefficient of linear expansion of steel
 = Change in temperature (Initial and final)
= Change in temperature (Initial and final)
Our values are,
Given that the length of each rail is
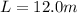
Initial temperature is
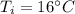
final temperature is
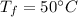
Coefficient of linear expansion of steel is
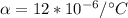
Replacing,
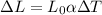
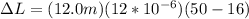
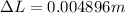
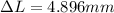
Therefore the gaps will be 4.896mm langer than its initial length.